Hi All , so in a previous article i tried to explain how D-H works , and i hope I did a good job of it and hopefully there’s no questions , but how hard would it be for the person eavesdropping to reverse the “secret exponents” and guess the key?

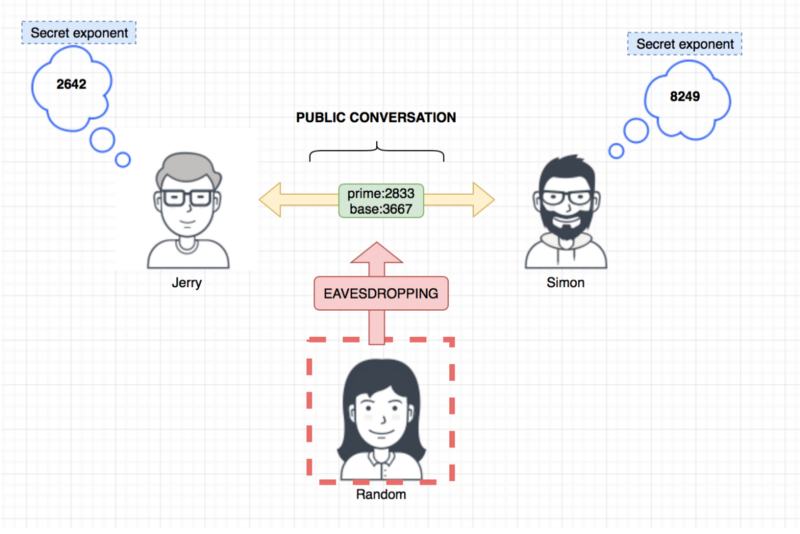image Initial communication

Remember that image ? let’s recap:

Jerry and Simon agreed a prime and a base number , while they were chatting about this there’s a third person “Random” that is listening to everything.

Next step Simon and Jerry will calculate a number and tell it each other, for example jerry will tell Simon:

BASE to the SECRET EXPONENT modulo PRIME

which translates to:

3667 ** 6531 % 2833 = 2642

So Jerry will tell Simon my Computed number is 2642.

So how hard is it for “Random” to obtain the “secret exponent” with all the values that she had right now? to clarify “Random” equation should be something like:

3667 ** **X** % 2833 = 2642

X is the value we want to know , if “Random” knows X , then she will be able to know the secret exponent.

This is called discrete logarithms , so to examplify this i will use smaller numbers:

BASE=5 , PRIME=7 , RESULT=2 , SECRET = 10  
**5 ** 7 % 17 = 10**

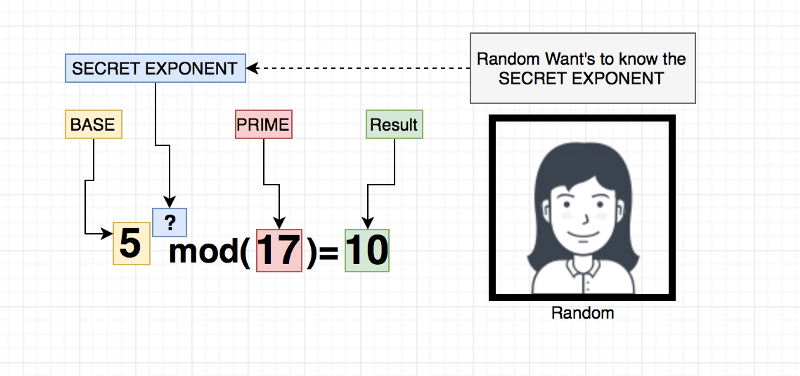
image

So far there’s no easy way to solve this backwards , it’s easy with small numbers , for example we could make a list of all numbers smaller than prime:

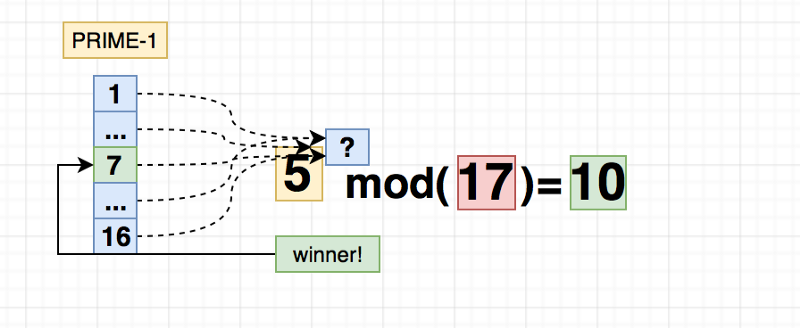
image

So that would work in a way … but as you can tell it is sort of brute forcing , the catch is when you use a large prime number (+100 digits) , something in the range of:

2074722246773485207821695222107608587480996474721117292752992589912196684750549658310084416732550077

you can see the complexity increases drastically , the other catch is once you build this table , and build it in time! , how do you search efficiently over it ? as you see not impossible but very very slow.

So long prime numbers would add a lot of complexity to the reversing this modulo.

One question that in a forum was how complex is to generate these numbers , and how fast is it ? specially power of something.

Well what i found is that if the a compute want’s to know:

3 ** 17 OR 3 power of 17

The computer won’t do this: (it’s too slow)

3x3x3x3x3x3x3x3x3....

Instead there’s an operation called repeated squaring , which simplifies this greatly , the idea is the following:

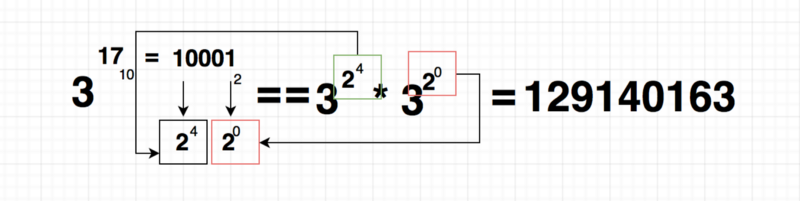
image

This is way faster than multiplying 3 , 17 times :)

So to wrap up , Some arithmetic operations are very easy/doable one way but very complex the other way around , hence D-H popularity .