D-H is a key exchange mechanism , a way to exchange cryptographic keys over public channels, that is , I want to agree a number with my buddy Simon but i don’t want to tell him what the number is.

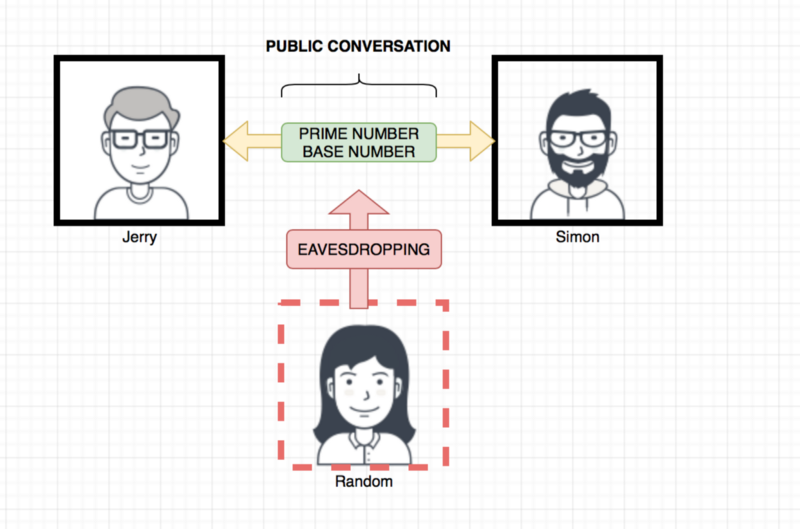image Agreeing in Prime and Base Numbers

So there is a few requirements for this to work , and also a bunch of rules that have to be applied to the values we gonna communicate over an open space:

  • Agree a Prime Number
  • Agree a Base Number
  • 1 secret exponent each

So all these numbers are communicated to each other over public transport , and this is the requirement: Each user will generate a “secret exponent” that can’t have any common factors between them. So here’s some code to make this up

def giveMePrimes():  
  primeList = list()  
  for num in range(1000,10001):  
    if all(num%i!=0 for i in range(2,int(math.sqrt(num))+1)):  
      primeList.append(num)  
  return primeList

This appends the the prime numbers in the range() to a list.

For the Base and Secret Exponents we pick numbers just randomzingin a range:

secure_random.choice = random.SystemRandom()  
secure_random.choice(range(1,10001))

Let’s assume we have these numbers:

P (prime) = **2833**  
N (base) = **3667**  
J(Jerry's Secret exponent) = **6531**  
S(Simon's Secret exponent) = **8249**

Only the secret exponent are the ones we want to keep private , Jerry and Simon know only their “secret exponent” ,P and N , in short only P and N have been communicated over public channels.

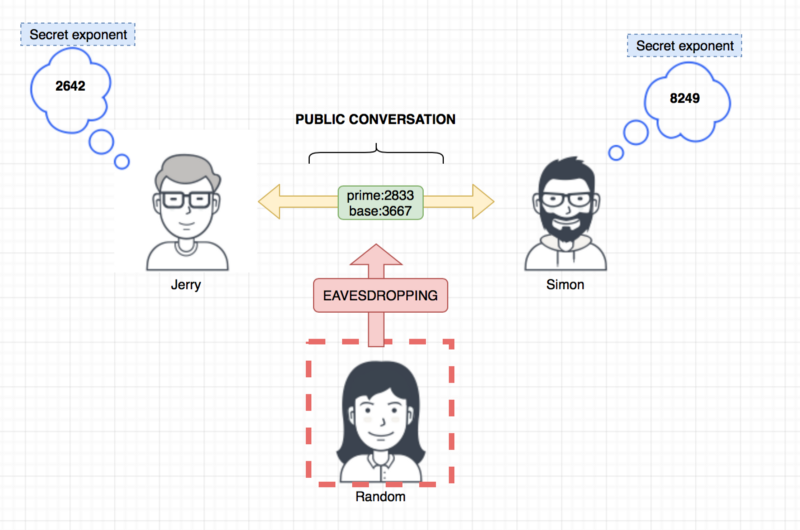
image

Now each party will compute a number with the values they have (P , N and each individual “secret exponent”)

Jerry will compute: (N(base) to the J(secret exponent) modulus P (prime))

JC = N ** J % P (**2642**)

and Simon:

SC = N ** S % P (**1037**)

And they will pass each other these values (Jerry passes JC to Simon , and Simon passes SC to Jerry).

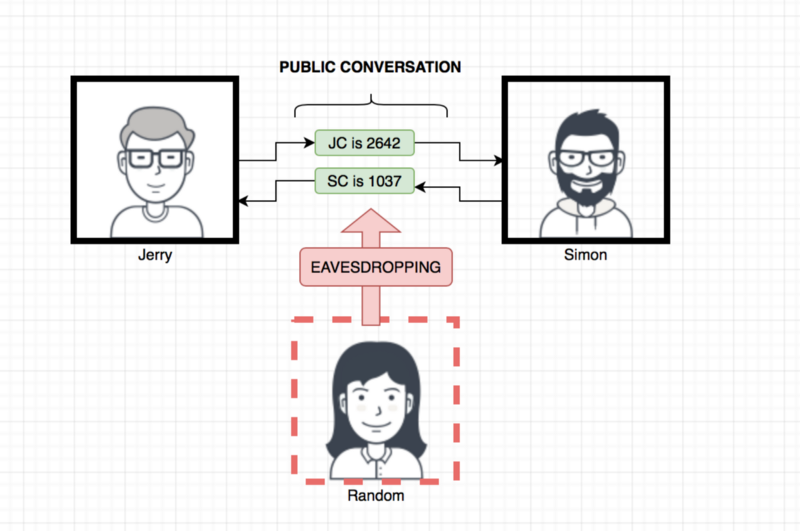
image

Good ! so now to Recap , let’s see what values each individual knows:

Jerry: Prime , Base , Jerry’s secret exponent , JC and SC

Simon: Prime , Base , Simon’s secret exponent , JC and SC

Random: Prime , Base , JC and SC

So now is when the magic happens , both of them apply the following function: ( peer’s computed number to the “secret exponent” modulus Prime)

Jerry:

SC ** J % P

Simon

JC ** S % P

And if you do the math this translates to:

Jerry

1037 ** 6531 % 2833 = 1747L

Simon

2642 ** 8249 % 2833 = 1747L

Great (L == Python’s literal ) , now we have have a number(1747L) that Simon and Jerry know that derived of a bunch of numbers that were transmitted publicly.

With this number as a “key” Simon and Jerry can start communicating privately using a cipher.