Hi Guys , last article we spoke about addition , one of the most important “invented” operations on eliptic curve arithmetic . There’s been great feedback highlihghting that the rule “if a line crosses two points , it will cross a third point” might not be absolute.

That’s is true , there’s a few exceptions and today I will try to explain one , what would happen if point P and Q share the same position (x and y wise):

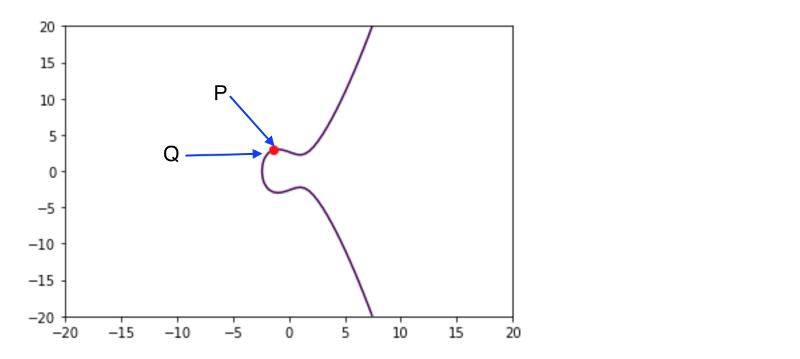image P and Q sharing position

So how do you add two points (P and Q ) that share the same location? , well this is called “Point Doubling” also referred as adding a point to itself.

This is nothing more than another invented operation and as we saw in EC addition it is represented by another mathematical identity , as well as a different “Slope” equation.

Point Doubling Slope:

To calculate the slope when P == Q we apply the following equation:

s = (3 * Px ** 2 +a ) / (2 * Py)

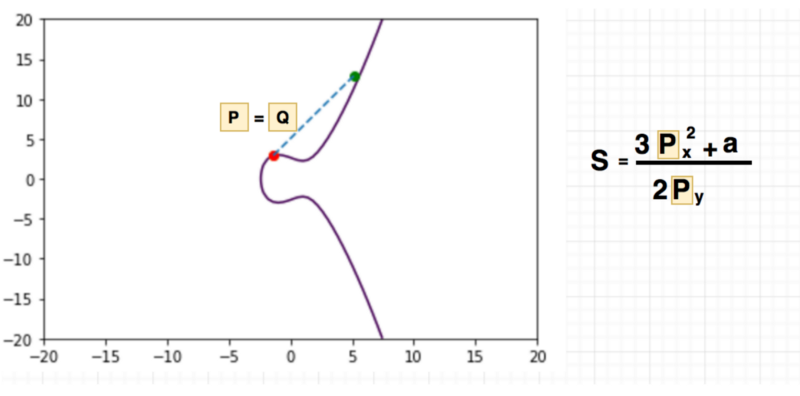image Slope in point doubling

That will give you the value of the slope , remember that the slope plus some other domain parameters are curcial to then caculate addition or in this case point doubling.

Point Doubling:

Point doubling or “adding a point to itself” follows a very simple equation , and of course it requires the slope and the domain parameters that we’ve seen in previous articles.

But basically it goes like this:

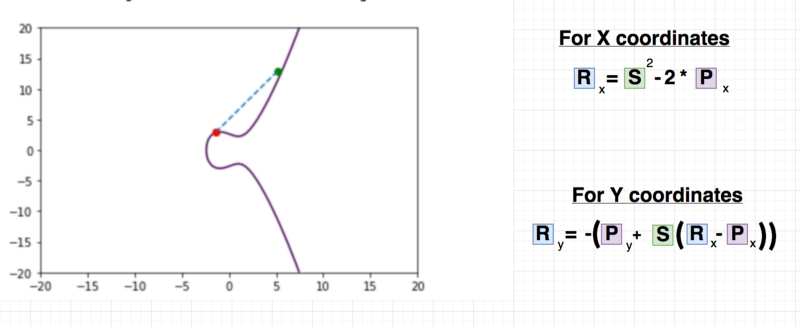image Point Doubling in action

RX = S ** 2 - 2 * PX  
RY = -1 * (PY + S * ( RX - PX))

And again the same catch , R becomes the negative reflection of R , so it looks something like:

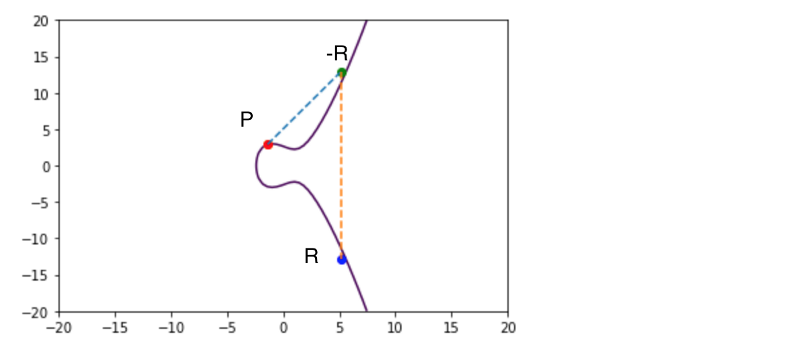image Reflection of R

Conclusion:

So point doubing is the second invented arithmetic operation we’ve talked about when it comes to Elliptic Curves , and some of the same rules apply than with addition:

  • by knowing X you know Y
  • R is the reflection of -R over the X axis

Some gisted code so you can have a play:

PS: Thanks for all the comments and questions