Alright! , so we’ve talked about D-H and RSA , and those we’re sort of easy to follow , you didn’t need to know a lot of math to sort of grasp the the idea , I think that would be a fair statement.

Well things are a little bit steeper when facing ECC , to say the least , it’s got multiple properties and there’s a lot more math in it . I want to divide these series into 3 parts because I am discovering it myself as I go.

Why Elliptic Curve?

ECC is a public key based , such as RSA , but it is sort of represented in an algebraic structure , ECC offers the same security than RSA but at a smaller footprint , also it’s less cpu intensive so it’s ideal for mobile devices and faster acting networks.

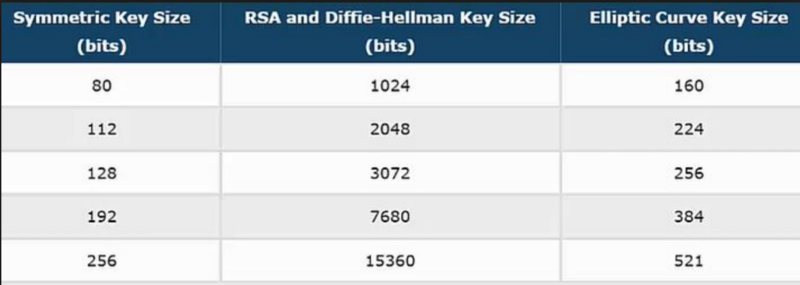image RSA vs ECC

What’s an Eliptic Curve?

By definition :

In mathematics, an elliptic curve is a plane algebraic curve defined by an equation of the form. that is non-singular; that is, it has no cusps or self-intersections.

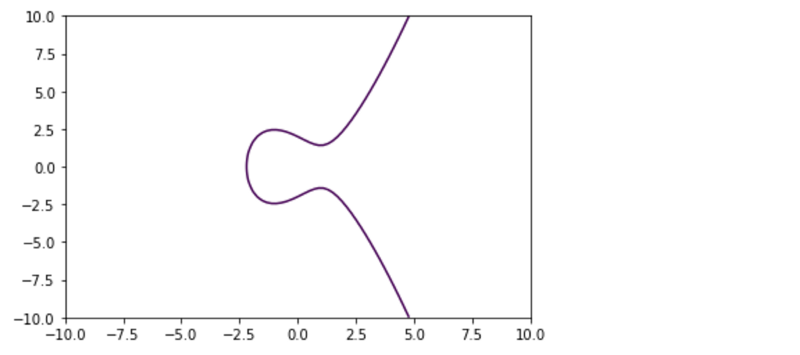
So it really a curve where all the points (x,y coordinates) satisfy an equation , it is really that simple , well not that simple.

How does it look and what’s the equation?

Well the nice way to represent it is something like:

image

The equation that all points in this Curve should satisfy would be something like

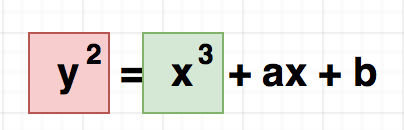
image

y ** 2 = x ** 3 + ax +b

So in theory , if you make a list of a lot of “y” coordinates (real numbers) and apply that equation to all of them , you should obtain a curve looking sort of like that.

Now for most of this work I’ve been using :

I highly recommend these .

Let’s make a Curve!

Before we plot a list of points of real numbers that honour the equation let’s clarify that when the fact that the equation suggest y square , means that the negative and positive Y axis of the curve will be the same, that is that if a point exists in y:4 it will also exit in y:-4 , you can see it in the curve above:

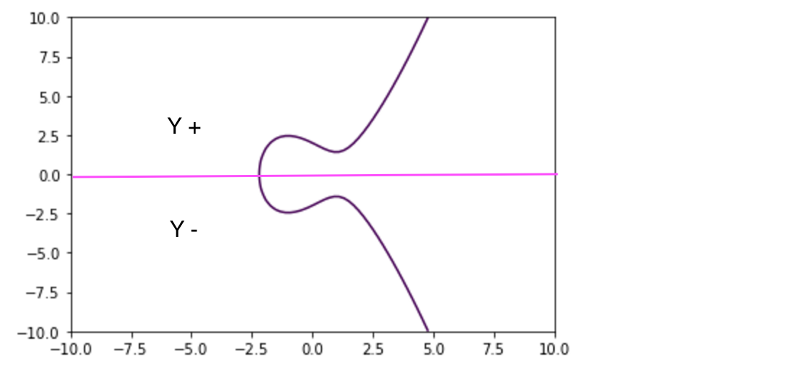
image

Cool , so now let’s see if this thing is true , the following code is what I’ve used in jupyter to get thee graphs I’m showing here

I’ll go step by step:

f(x) = x ** 3 + 3x + 4

This is the most important part really , remember the equation that defined the curve? So this is one side of it , as you can see “a = 3” and “b = 4” , these parameters are called domain parameters , and they decide a various attributes of the curve.

Also , the equation has to return something else than 0 , so we can sort of graph it out hence:

if res > 0

One more thing , notice that the result of the equation has to be square rooted becase y was square , so we do the following:

ys.append(np.sqrt(res))

So what does this look like?

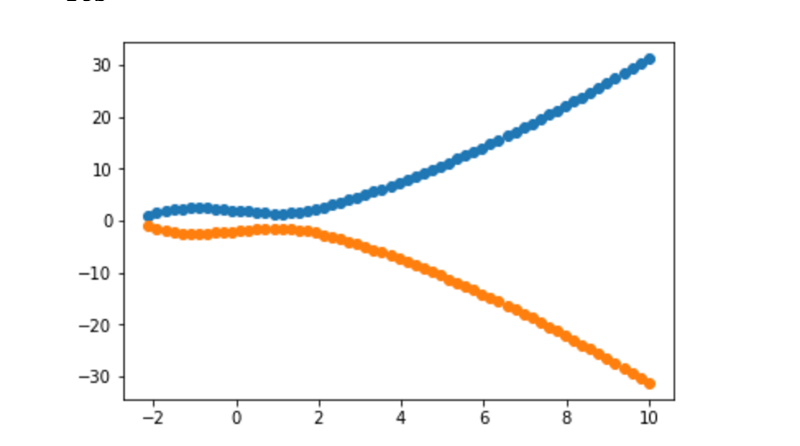
image

Yea ok , it isn’t great but it sort of resemble the curve we were looking at before.

Matplotlib comes with a really fancy function called contour , which accepts an equation , so we can do the following:

And this turns into this:

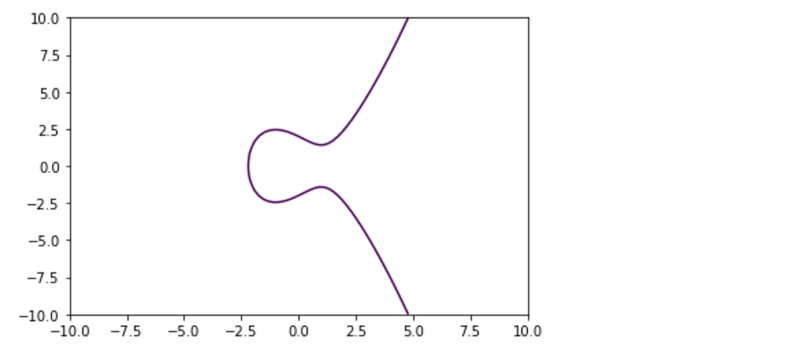
image

One final property of this curve:

This is probably the most important property of this curve , and it is that if a line intersects two points in the curve it will always intersect a third.

This is very important , since that third point will be the representation of the public key , remember that all this hassle is to create public keys from a private key , that at this point are massive prime numbers.

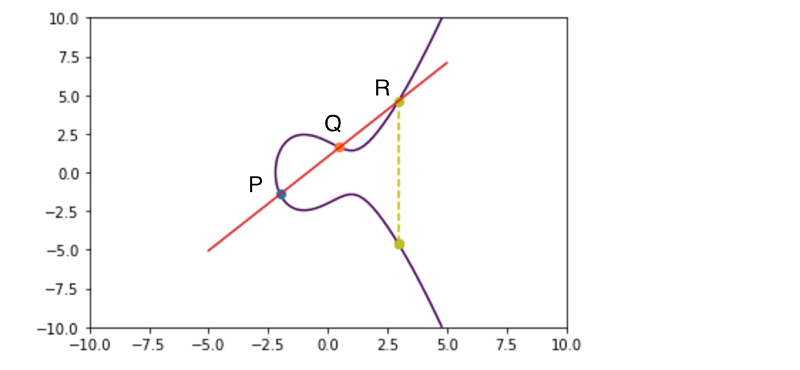
image

So you see how one line crossing two points in the curve (P,Q) always intersects another (R).

To sum up today’s article

  • Points in a curve satisfy an equation
  • Based on the equation knowing “X” you will ultimately know “Y”
  • The curve is identical on the Y axis
  • If a line can intersect two points in the curve will also intersect a third one
  • Domain parameters affect various attributes of a given curve
  • Use Jupyter!