Hey guys , I wanted to write a little bit about RSA cryptosystem .

RSA is an asymmetric system , which means that a key pair will be generated (we will see how soon) , a public key and a private key , obviously you keep your private key secure and pass around the public one.

The algorithm was published in the 70’s by Ron Rivest, Adi Shamir, and Leonard Adleman, hence RSA , and it sort of implement’s a trapdoor function such as Diffie’s one.

RSA is rather slow so it’s hardly used to encrypt data , more frequently it is used to encrypt and pass around symmetric keys which can actually deal with encryption at a faster speed.

How does it work?

As in D-H I’m gonna be using rather small numbers, but keep in mind that the real value of most of mod(p) based algorithms happens when huge primary numbers are used.

The first part i’ll show how the trapdoor function works , and then i’ll explain why it works , so bare with me.

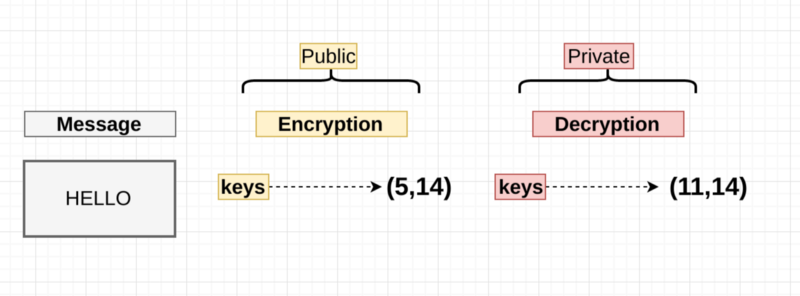image Essentials

We’ve got a message (“HELLO”) , and we’ve picked two tuples with two numbers each ( I will explain how these came about later). Obviously there’s no arithmetic operation we can perform with strings , so the message has to be convert it to something , so let’s say “HELLO” converts using some conversion algo to “2”

Normally , in production , a lot of different techniques are used to encode the message and padding is also used

Ok Fantastic we have everything we need , let’s run the message through the functions that will in theory encrypt this for us:

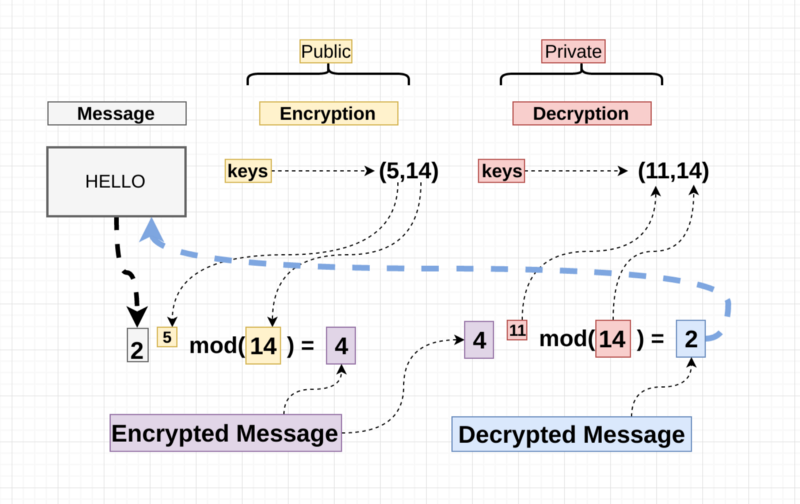image mini rsa

So there we have the basics of the RSA algorithm , and how the trapped function is laid out.

The interesting bit is how we come about those numbers , and how (5,14) is related to (11,14), and this is the interesting part i believe , let’s start:

The details of the Decryption/Encryption pair:

  1. Pick two prime numbers , I will pick 2 and 7 , lets call them p and q
**P** = 2 and **Q** = 7
  1. Multiply P and Q , and that becomes the modulus
**N** = P * Q = **14**
  1. Make a list between 1 and 14 **** and remove the common factors:

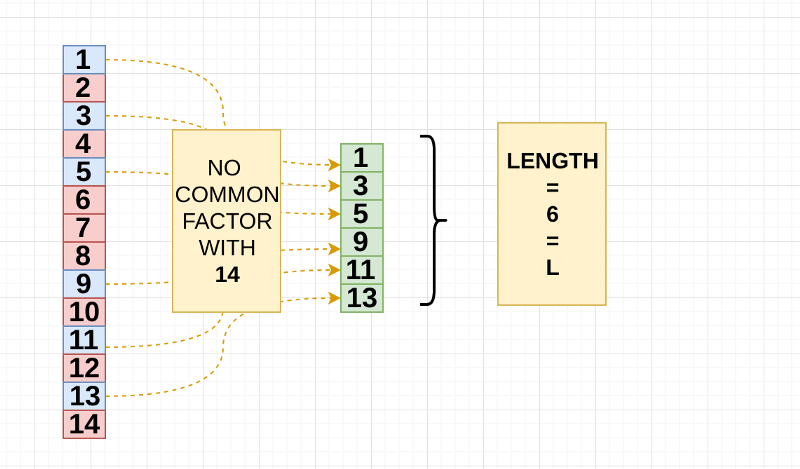
image

Now there’s an easy way to get this and that is:

( **Q** - 1 ) * ( **P** - 1) = **L**

(7 - 1 ) * ( 2 -1 ) = **6**

Great let’s save this number , let’s call it “L”

  1. Now we get to pick the encryption key , in the example was (5,14) , we know 14 is the modulus.

So for the encryption key there’s a few rules:

  • it’s got to be between 1 and L
[2,3,4,5]
  • Coprime with L (6) and the Modulus (14) , the answer is 5 , there’s no other possibility .

So there we came to a conclusion of why we picked (5,14)

  1. The Decryption part , In the example we’ve picked (11,14) , again 14 is the modulus but where does 11 come from?? , from now on let’s call it D , let’s find out why D is 11:

D has to follow one rule and this is it:

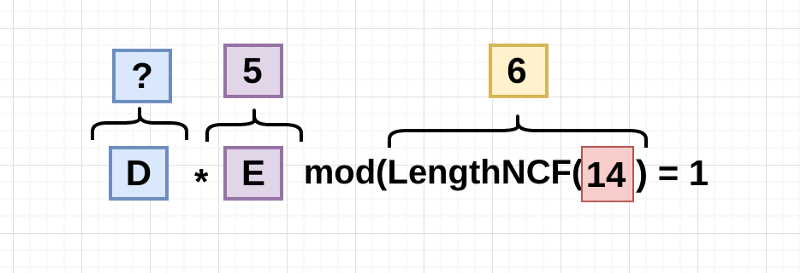
image

So the Decryptor(11) multiplied by the Encryptor(5) modulus the length of the non coMmon factor with the modulus(14) has to be equals to 1.

**D** * **E** % **LNCF**(N) = **1**  
11 * 5 % 6 = 1

So we know if we multiply D * E and E is 5 , D will need to be a common factor of 5 , so:

image

So I’ve made a list of numbers from 1 to 50 and , filtered the ones that when multiplied by E and moduled by LNCF(N) are equals 1 , so let’s see if those can decrypt the message :) , Remember the encrypted message is “4”,and the decrypted message is “2” so the function should be something like:

4 ** D % 14 = 2 <---Decrypted message

So let’s do a little list comprehension to see if the rule works:

image

Great ! it worked , you see how applying the function to all the Decryption keys that follow the rule (D * E % LNCF(N) = 1) , decrypted the message successfully .

I hope this didn’t get too complex , it certainly felt a bit complex but i tried to keep it as simple as possible .